分类已知类别，聚类未知类别。

概念

聚类，就是将样本划分为由类似的对象组成的多个类的过程。
聚类后，我们可以更加准确的在每个类中单独使用统计模型进行估计、分析或预测；也可以探究不同类之间的相关性和主要差异。

K-means

  1. 指定需要划分的簇[cù]的个数K值（类的个数）;
  2. 随机地选择K个数据对象作为初始的聚类中心（不一定要是我们的样本点）
  3. 计算其余的各个数据对象到这K个初始聚类中心的距离，把数据对象划归到距离它最近的那个中心所处在的簇类中;
  4. 调整新类并且重新计算出新类的中心;
  5. 循环步骤3和4，看中心是否收敛（不变），如果收敛或达到迭代次数则停止循环;
  6. 结束。

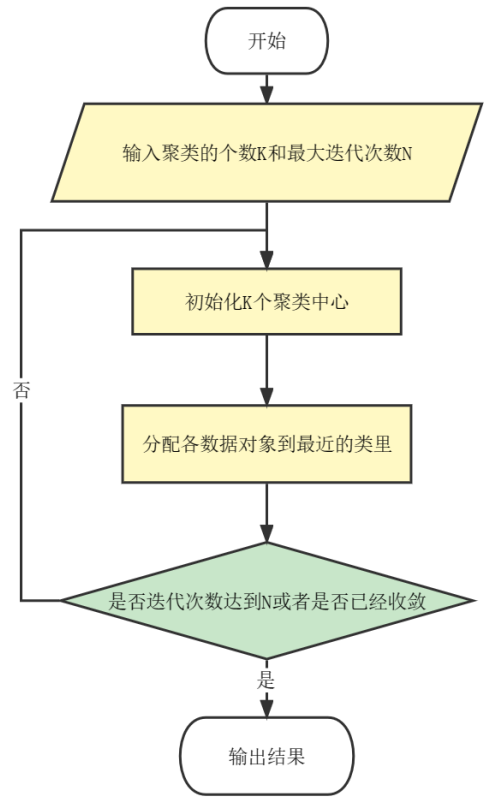
优点：简单、迅速、对处理大数据集高效率。
缺点：要求用户必须给出K、对初值敏感（最终聚类效果和一开始选择的聚类中心有很大的关系）、对于孤立点数据敏感。

改进：K-means++算法可以解决缺点2和3

K-means++

只对K-menas里“初始化K个聚类中心”进行了优化：

  1. 随机选择一个样本作为第一个聚类中心；
  2. 计算每个样本与当前已有聚类中心的最短距离（即与最近一个聚类中心的距离），这个值越大，表示被选取作为聚类中心的概率较大；最后，用轮盘法（依据概率大小来进行抽选）选出下一个聚类中心；
  3. 重复步骤2，直到选出K个聚类中心。选出初始点后，就继续使用标准的K-means算法了。

基本原则：初始的聚类中心之间的相互距离要尽可能的远。

SPSS操作步骤

K-means（默认使用K-means++）:

graph LR
A[分析] --> B(分类) --> C(K-均值聚类) 
C--> D(放入变量) 
C--> E(写入K) 
C--> F(迭代:更改N) 
C--> G(保存:勾选聚类成员和与聚类中心的距离)
C--> H(选项:勾选初始聚类中心和每个个案的聚类信息)

讨论

  1. 聚类的个数K值怎么定？
    答：分几类主要取决于个人的经验与感觉，通常的做法是多尝试几个K值，看分成几类的结果更好解释，更符合分析目的等。
  2. 数据的量纲不一致怎么办？
    答：如果数据的量纲不一样，那么算距离时就没有意义。例如：如果X1单位是米，X2单位是吨，用距离公式计算就会出现“米的平方”加上“吨的平方”再开平方，最后算出的东西没有数学意义，这就有问题了，需要计算标准值。

zi=xi−xˉσx(先减去均值再除以标准差)z_{i}=\frac{x_{i}-\bar{x}}{\sigma_{x}}\text{(先减去均值再除以标准差)}

SPSS操作：

graph LR
B(分析) --> C(描述统计) --> D(描述)-->E(勾选将标准化值另存为变量)

系统（层次）聚类

绝对值距离 (网格)
欧氏距离 (常用)

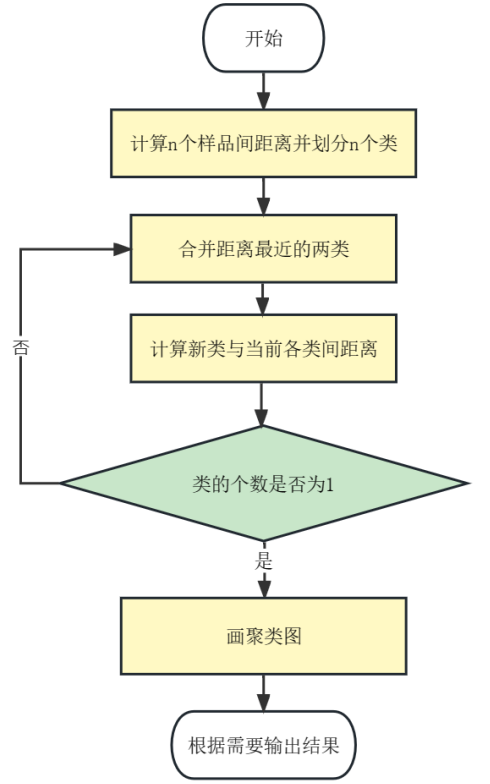
SPSS操作：

graph LR
A[分析] --> B(分类) --> C(系统聚类) 
C--> D(放入变量) 
C--> E(图:勾选谱系图)-->E1(根据聚合系数确定要分几类并说明) 
C--> F(方法:一般保持默认就可以) 
C--> G(统计与保存:可以更改分几类)

DBSCAN算法

基于密度的聚类方法 用的很少

总结

一般情况下还是用系统聚类 只有两个指标且作图发现很DBSCAN时再用DBSCAN聚类